function | domain and range

Function

Suppose that A and B be any two nonempty set. A operation  f : A → B is called a function from set A to set B if

• all the element of set A is related to the elements of set B.
• its mandatory that all the elements of set A should related with elements of another set.
• each of the elements of set A is uniquely mapped with the elements of set B.

for example let's take  A={a,b,c,d} and B={1,2,3,4} then 

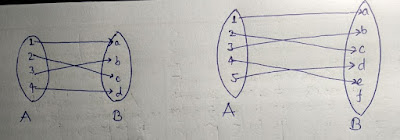
• In given figure f1 is a function according to the definition as a maps to 2,b maps to 1,c maps to 4 and d maps to 3.
• f2 is also a function according to definition as a maps to 1,b maps to 2,c maps to 3 and d maps to 4.
• f3 is also a function and each elements of set A is uniquely mapped with elements 1 of B.
• f4 is not a function as the element a of set A is not uniquely mapped with the elements of set B.
• f5 is also not a function because the element d of set A does not mapped with any elements of set B.

Domain, Co-Domain and Range

Suppose  f : A → B be any function then Set A is called as the Domain of the function f, Set B is called as Co-Domain of function f. Set of elements of B which is the pre-image of set A under function f is called as the Range of function f ; i.e. Set of f(A) is the Range of the function f.

Problem

Consider A={-1,0,1} and B={0,1,2,3,4} and suppose that a function f(x)=x^2. then,

f(-1)=(-1)^2=1, f(0)=(0)^2=0 and f(1)=(1)^2=1

we can see here that each elements of Set A is uniquely mapped with Set B. hence f : A → B defined by f(x)=x^2 is a function.

Clearly the domain of function is {-1,0,1}, co-domain of function is {0,1,2,3,4} and the range of the function is {0,1}.

Equality of two function

two function f and h are said to be equal if and only if

• domain of h = domain of f
• co-domain of h = co-domain of f
• h(x) = f(x) for all x belongs to their respective domain.

For Example Let   f : R→ R and g : R→ R be such that f(x) = x and g(x) = x^2/x for all x belongs to R(set of Real No.) 

Then we see that both function have the same domain and codomain in Set of Real Numbers and also both f(x) = g(x) for all x belong to respective domain of respective function; i.e. Set of Real Number.

Number of function

let A and B be two non-empty set having m and n elements respectively then the total number of function from Set A to Set B is equal n*n*n*............*n (m-times) that is equal to n^m.

Total number of Relation from Set A to Set B = 2^mn

Total number of Relation that is not function = 2^mn - n^m

One-One Function (Injective Function)

Let  f : A → B be any function then the function f is called one-one 

⟺f(a) = f(b) implies a=b for all a∈A and b∈b

⟺a ≠ b implies f(a) ≠ f(b)

injective function

Example:  Let A={1,2,3} and B={1,2,3,4,5} and let  f : A → B be any function defined by f(x)=x+1 for all x∈A then we can observe that f ={(1,2),(2,3),(3,4)}.

Its clear that all the different elements of A have different image under the given function. hence, function f is an injective/one-one function.

Number of One-One Function

If A and B be any two non-empty set having m and n element respectively.Then the number of one-one function from Set A to Set B =nPm if n≥m And 0 if n<m

where nPm is permutational format where nPm=n!/(n-m)!

Note

1. If f : A → B is an one-one function then the graph of the given function i.e.y = f(x) will be strictly decreasing or strictly increasing; i.e. dy/dx<0 or dy/dx>0
2. If we draw a line parallel to X-Axis on the given function's Curve if there will only one intersecting point of the line on the given curve the function will be one-one but if the line cut the graph on distinct point function will not be injective.

Ex:

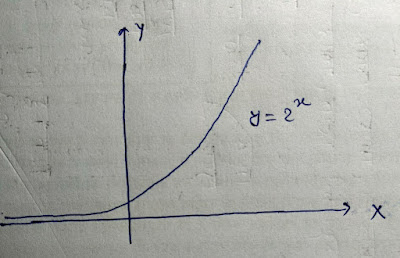
Let f : R→ R be any function such that f(x) = 2^x As the graph of given function is strictly increasing so by the first result we can conclude that f(x) is one-one/injective function.

one-one function

Let f : R→ R be any function such that f(x)= X^2 then we see that by the figure if we draw a line parallel to X -Axis there will be two intersecting point so the function will not be one-one function.

Onto Function (Surjective Function)

Let  f : A → B be any function then the function f is called onto If every elements of Set B is the pre-image of some element of set A under the function f; i.e. B = f(A) 

onto and not onto function

Number of Onto Function

If Set A has m elements and Set B has n elements, the number of onto functions are given by the following formula

n^m-[nC1](n-1)^m+[nC2](n-2)^m........(-1)^n-1[nCn-1]1^m   

Eg. Let A={-3,-1,1,3} and B ={1,9} and Let's define a function f : R → R such that f(x)=X^2 then f(A)={f(-3),f(-1),f(1),f(3)}={1,9} so the function will be Onto.

Bijection Function(One-One Onto Function)

Let  f : A → B be any function then the function f is called Bijective function/One-One Onto function if It is Both One-One and Onto function. 

Number of Bijective Mapping 

Let  f : A → B be any bijective function then the Cardinality of both the set A and set B will same. Let's take Cardinality is m then the no. of bijection will be m! 

Constant Function 

Let  f : A → B be any function then the function f is called constant function if f(x)=c where c is any constant number and c∈B for all x∈A.

constant function

Note

• Constant Function may be one-one or many-one, onto or into
• Range of constant function contains singleton set or only one element.

Identity Function

Let  f : A → B be any function then the function f is called Identity function ⟺ f(x) = x for all x∈A. Identity function is denoted by I. Identity function is a Bijective function too.

identity function

Related Posts😍👇

Matrix | Linear Algebra

Set Theory Introduction | Definition Of Sets

I hope you can understand the very important topic function. give your feedback and suggestion .it will be the most welcome. In case of any doubt contact with us or ask in comment section. Thankyou